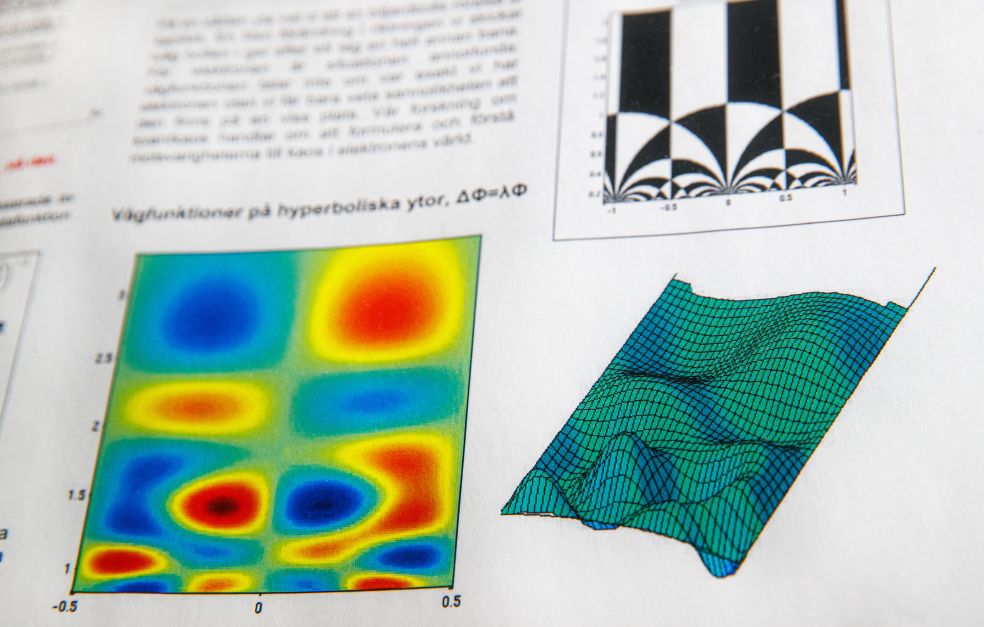
The abstract world of mathematics offers many challenges. As a Wallenberg Scholar, Andreas Strömbergsson has the opportunity to adopt a new approach to complex mathematical problems. His research centers on the overlap between number theory and dynamical systems, often relating to classical problems that are several hundred years old.
Andreas Strömbergsson
Professor of Mathematics
Wallenberg Scholar
Institution:
Uppsala University
Research field:
The overlap between number theory and dynamical systems, in particular homogeneous dynamics. Further development and creation of new mathematical methods for various limit problems in homogeneous spaces.
Strömbergsson is based at the Ångström Laboratory at Uppsala University. Research in mathematics here has increased in strength in recent years.
“I notice in my contact with fellow researchers around the world that Uppsala has become a force to be reckoned with in the mathematical field.”
As a professor, Strömbergsson spends some of his time supervising and teaching the next generation of mathematicians, but most time of all he spends thinking.
“Arguably the most important thing for a mathematician is to have the time to sit down in peace and quiet and ponder knotty problems.”
Delving deep into mathematical research can be quite lonely, but also highly stimulating.
His research on number theory and dynamical systems focuses particularly on homogeneous dynamics. This may be described as studying a system in which all the parts behave in a uniform manner in time and space.
“I divide my work up into small sub-problems that I wrestle with.”
New insights
Many of the questions that Strömbergsson is studying involve mathematical models for moving or stationary spheres, often related to classical problems. One example is the “hard-sphere model,” a fundamental model in gas theory originally formulated in the 19th century by physicist Ludwig Boltzmann.
The model describes gas particles as a multitude of identical solid spheres moving in a container. These spheres travel in straight lines at a constant velocity until they collide with each other or the sides of the container. They interact according to simple rules, colliding with each other elastically before going on their way.
Despite its simplicity, the hard-sphere model has given rise to deep mathematical questions. Endeavoring to understand how numerous spheres of this kind behave over time entails complex equations and theories.
“In some versions of the model it’s possible to use homogeneous dynamics to describe how the system develops. We hope that further research will bring us closer to a solution and provide precise mathematical proof.”
Packing oranges in higher dimensions
Another classical question concerns the sphere packing problem. The challenge is to determine the most space-efficient way of packing identical spheres – perfectly spherical oranges, for instance.
The issue relates to a historical problem – The Kepler Conjecture, dating back to 1611. The problem remained unsolved for hundreds of years; it was not until 1998 that Thomas Hales published a 250-page paper setting out the mathematical proof for the optimal packing of three-dimensional spheres.
In recent years Maryna Viazovska (with collaborators) has published a proof for optimal packing of eight- and 24-dimensional spheres. But the problem gets much more complicated at higher dimensions.
“If we pack oranges in spaces with a hundred, thousand or even a million dimensions, we know surprisingly little about the optimal packing density. The difference between the best-known upper and lower limits of the density is huge.”
Strömbergsson wants to bridge this gap in our knowledge, specifically by studying lattices of regularly arranged points. He hopes that understanding the properties of lattices in higher dimensions will enable him to piece together an understanding of this problem.
Statistical properties of sequences of numbers
Strömbergsson can use results from homogeneous dynamics in combination with other methods to understand various mathematical problems. One field that interests him is the statistical properties of sequences of numbers that form specific patterns.
One example is to study the fractional parts of square roots of natural numbers, such as the root of 2, the root of 3, and so on. By treating these fractional parts as points on a line of numbers between 0 and 1, it is possible to analyze the distance between adjacent points.
It transpires that the distances are not randomly distributed. A specific statistical distribution occurs for square roots, whereas for other roots, such as cubic roots, there is a different distribution, often exponential.
“This type of analysis has links to quantum mechanics, particularly as regards the energy levels in a quantum system.”
Strömbergsson’s research aims to gain an understanding of the underlying mathematical structures, thereby providing insights into the ways that complex systems behave at macroscopic level.
Driven by curiosity
Strömbergsson stresses the importance of pure scientific research – seeking knowledge for its own sake without immediately considering potential applications. He points out that a large part of scientific progress is driven by curiosity and the desire to understand the unknown.
He concedes that researching in such abstract fields is a challenge, and that it is not always easy to explain the research to the uninitiated. He usually takes great pains to be as clear as possible when writing popular scientific summaries.
“Many people ask what the practical utility of the research is, and it’s not an easy question to answer. For my part, it’s about developing our understanding of mathematical structures.”
At some point in the future this research may lead to unexpected applications, which Strömbergsson also looks forward to. But most of all he enjoys his day-to-day life as a researcher, especially as he now has more time to spend on solving problems.
Text Nils Johan Tjärnlund
Translation Maxwell Arding
Photo Magnus Bergström